神经元不仅仅是一个开关
1876年,意大利物理学家Luigi Galvani在一次偶然实验中发现,静电可以让死青蛙的腿动起来。这一发现不仅揭示了神经系统对电信号的反应,也无意中探索到了控制青蛙肢体的“开关”。但实际上,生物体中神经元不只是开与关的关系,它们的相互作用要复杂得多。如这涉及膜电位变化、轴突传递等更复杂的过程*。
当神经元接收到足够的刺激时,细胞膜上的离子通道会打开,允许特定的离子(如钠离子Na+和钾离子K+)通过。这个过程导致细胞内外的电位发生变化,形成动作电位。动作电位的产生是一个全或无的现象,一旦达到阈值,电信号就会沿着神经元的轴突传递,最终通过突触将信号传递给下一个神经元。之后这个神经元需要休息一段时间(不应期,此时神经元对新的刺激不敏感,无法产生新的动作电位),才能够再次传递信号。
当下流行的神经网络,不论是图像识别的卷积神经网络(CNN),还是处理自然语言的Transformer,神经元的传递都被简化为一个开关操作。人工神经元的信号传递,是纯数学的,理论上可以立即完成(实际受限于计算机的处理速度)。然而,与忽略信号传播时间的主流人工神经网络不同,近年来备受关注的第三代神经网络——脉冲神经网络(SNN),则试图以更加仿真的方式,去模拟神经元的活动。
在SNN中,神经元的激活是通过脉冲序列来表示的,这些脉冲在时间上是有间隔的,而不是像传统的人工神经网络那样立即完成。这种时间编码方式使得SNN能够捕捉到输入信号的时间动态特性,这在处理时间序列数据或需要考虑时间依赖性的任务中尤为重要。
在SNN中,神经元的激活不是简单的开关行为,而是考虑了神经元膜电位的动态变化以及离子通道的开闭对电位的影响。当膜电位达到某个阈值时,神经元会发射一个脉冲,然后迅速复位到静息电位,这个过程称为“脉冲发放”。
然而,在当下的人工神经元中,决定神经元是否激活的函数,如sigmod或tanh,都是连续可微分的,而脉冲神经网络中的神经元则是阶跃函数,即当膜电位达到阈值时,神经元立即发射脉冲,否则不发放。这个阶跃函数在脉冲发射点是不可微的,因为它的导数在这一点上是未定义的。这使得训练脉冲神经网络变得不那么简单。
而最近的一项研究,来自NeuroAI的研究者不仅提出了一种能够训练脉冲神经网络的算法,还指出该方法在生物学上和大脑的神经活动遵循着同样的约束——即信息瓶颈。

https://doi.org/10.3389/fncom.2024.1240348
信息瓶颈——学到真知需要先忘记
信息瓶颈理论起源于信息论中的互信息概念(Mutual Information,衡量了两个随机变量之间的共享信息量),最早由Tishby提出*,后被用于解释人工神经网络的运行机制。现在,我们就用一个关于食品的双关比喻来说明信息瓶颈是如何揭开神经网络中神秘的面纱的。
Tishby, Naftali, and Noga Zaslavsky. “Deep learning and the information bottleneck principle.” 2015 ieee information theory workshop (itw). IEEE, 2015.
假如我们要制作一种特殊的压缩饼干,需要从各种面点中提取出最关键的成分来决定饼干的配方。这就像是我们需要通过一个特殊的“筛选器”来找出最重要的信息,这个过程就是信息瓶颈理论的核心。
在这个理论中,我们把所有面点的成分看作是输入(X),压缩饼干的成分是输出(Y)。首先,我们需要一个“编码器”来处理输入的面点成分,把它转换成一个中间的形式(T),这个过程就像是从各种面点中提取共性,去除不需要的差异,正如物理上的压缩一样。然后,一个“解码器”再把这个中间形式转换成最终的输出,也就是饼干的成分。
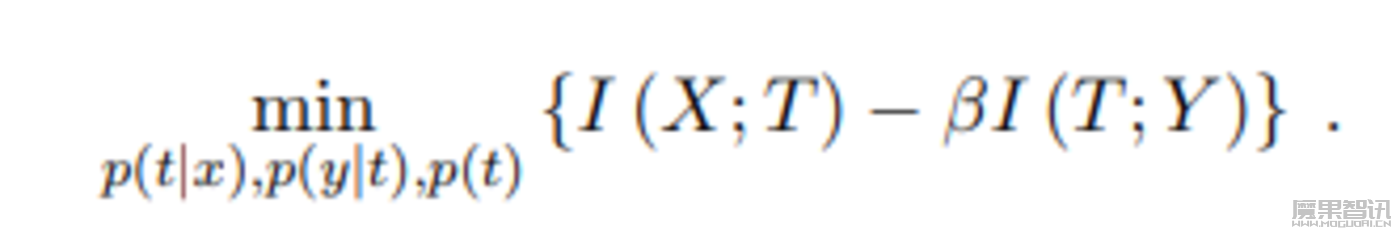
在这个过程中,有一个参数β,它决定了我们在筛选信息时,保留多少原始面点的信息。这就像是我们在做题时,决定在草稿纸上保留多少关键步骤一样。
通过这样的模型,研究者可以找到模型中的关键特征,优化决策过程,提升学习效率。在更复杂的多层神经网络中,每一层的处理也可以看作是一个小的信息筛选过程,其信息瓶颈问题可以通过Hilbert-Schmidt Independence Criterion(HSIC,如下图)来分析。
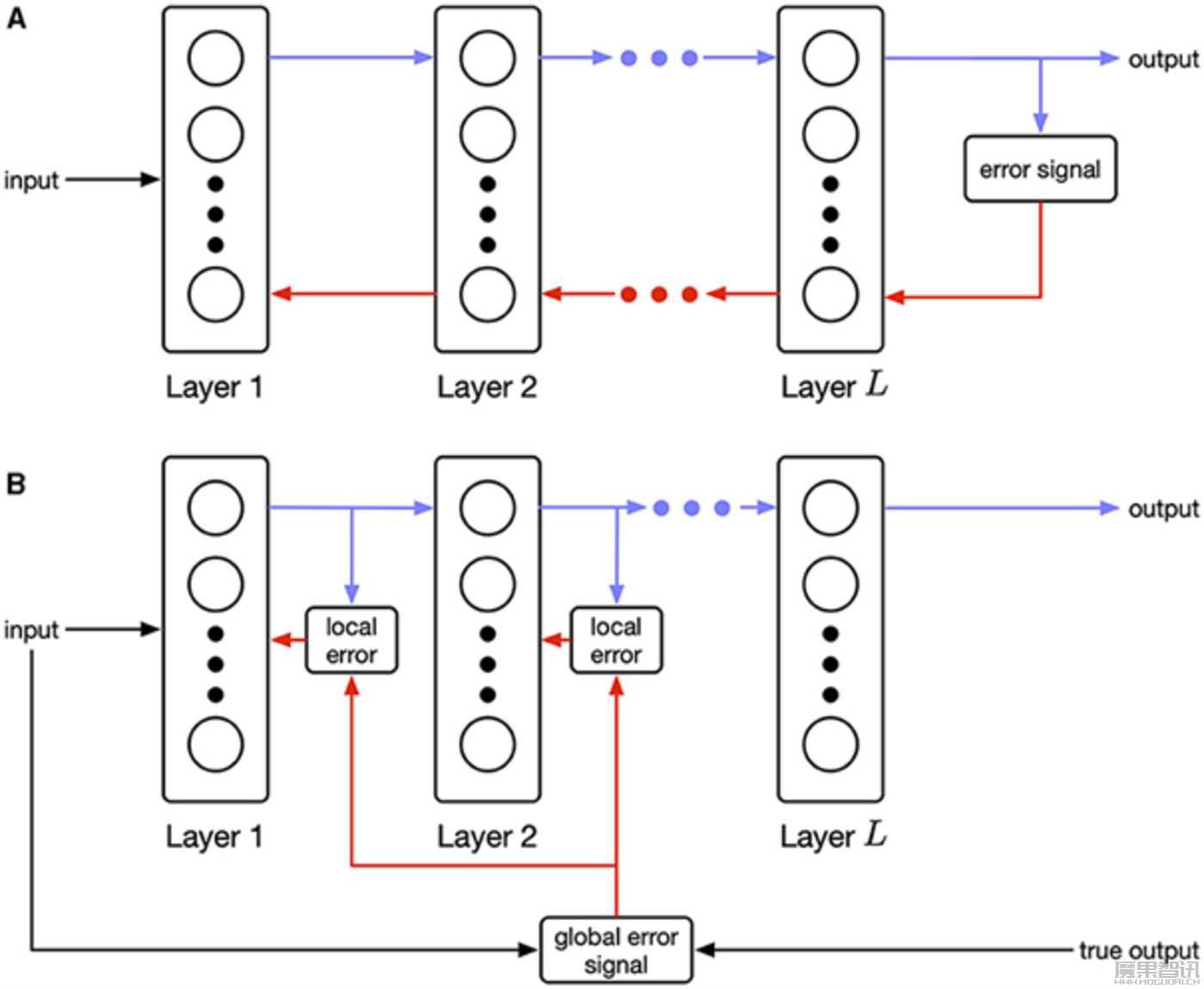
▷图1:(A) 顺序错误传播(传统的反向传播)要求层与层之间进行精确的信息逆向传递。(B) 并行错误传播则仅依赖局部信息,并结合全局调节信号。这种类型的生物学规则被称为三因素学习规则。
而要构建一个好的人工智能模型,我们需要给每一层网络足够的“临时存储空间”,就像我们做不同数学题时需要草稿纸一样。这可以通过一种叫做“储备池计算”(Reservoir Computing)的方法来实现。
储备池里面充满了随机稀疏连接的人工神经元。它们可以是传统的连续可微的,也可以是脉冲式的。而这个储备池中有多少个人工神经元,则可视为工作记忆的大小。我们通过调整这些神经元的连接强度,改善模型的学习效果。由此,一个生物学上符合类脑的脉冲神经网络如图2所示,而其中的学习规则是局部基于赫布法则和信息瓶颈来设置的。
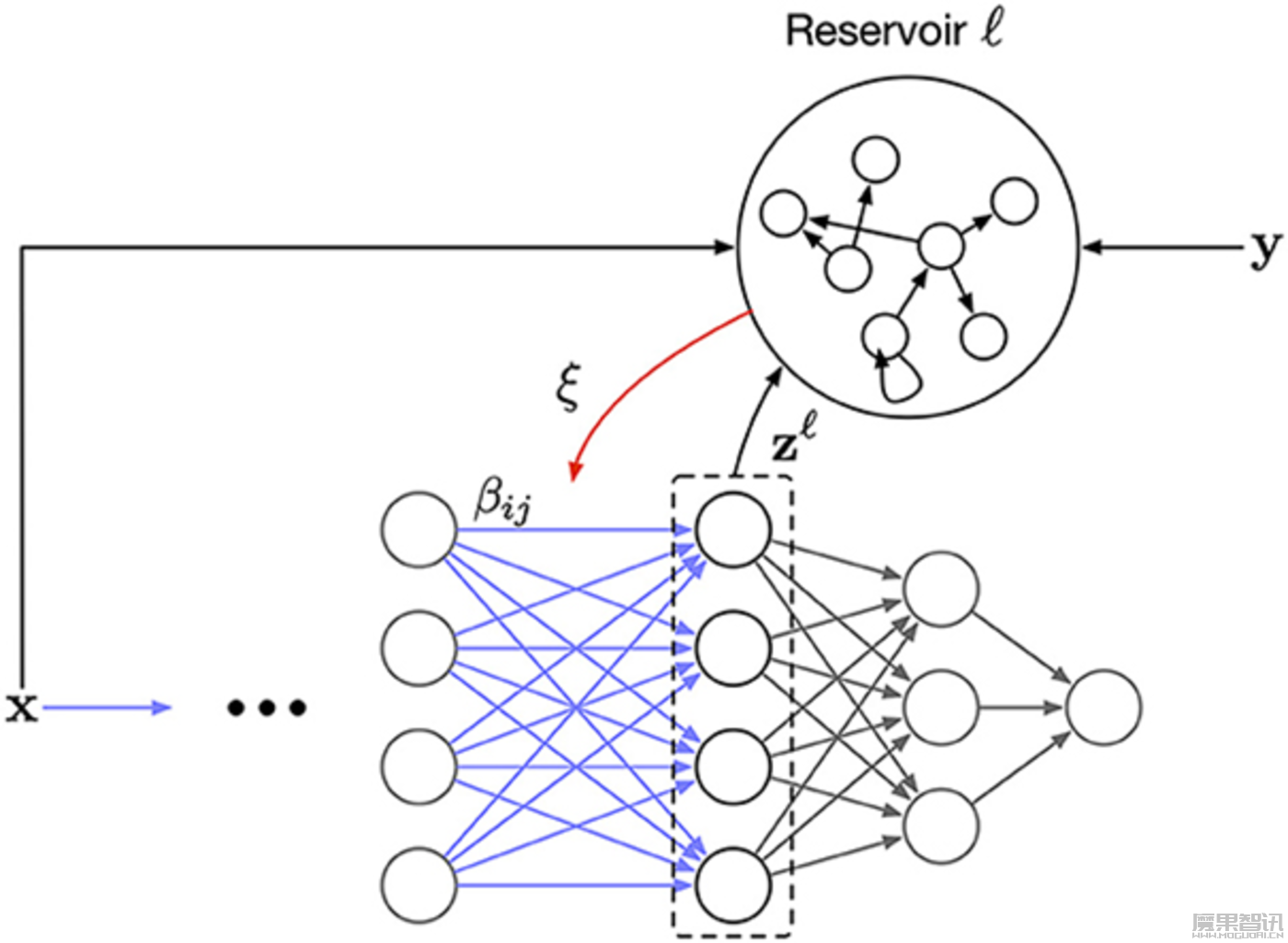
▷图2:整体网络架构如上图所示。每个层都配有一个辅助的储备网络。突触更新参数β受到一个层级的错误信号ξ的调节,这个错误信号是从储备网络中获取的。
我们再回到压缩饼干的比喻,假设我们有一个机器,它的任务是区分不同类型的压缩饼干。每种饼干都由不同比例的成分(如碳水化合物、蛋白质等)组成。我们注意到,某些成分经常会一起出现,比如碳水化合物和蛋白质。基于信息瓶颈原理,如果两种成分经常一起出现,我们就可以用更少的信息来记录它们。
而前面提到的“储备池”就像是我们在决定成分比例时用的草稿纸,帮助我们记录和计算信息。通过这样的学习和调整,我们的模型学会了一种识别压缩饼干的规则,多个规则组合后,就形成了识别压缩饼干的模型。
有待提升的学习规则
信息瓶颈的理念在用于图像分类的小数据集Minst已经展示出其效力,达到了91%的准确度,而在包含更多图片和类型的大数据CIFAR-10上,该模型也取得了大约61%的准确率,如图3所示。尽管与传统方法存在差异,但这一成果验证了信息瓶颈原则在处理复杂数据中的应用潜力。
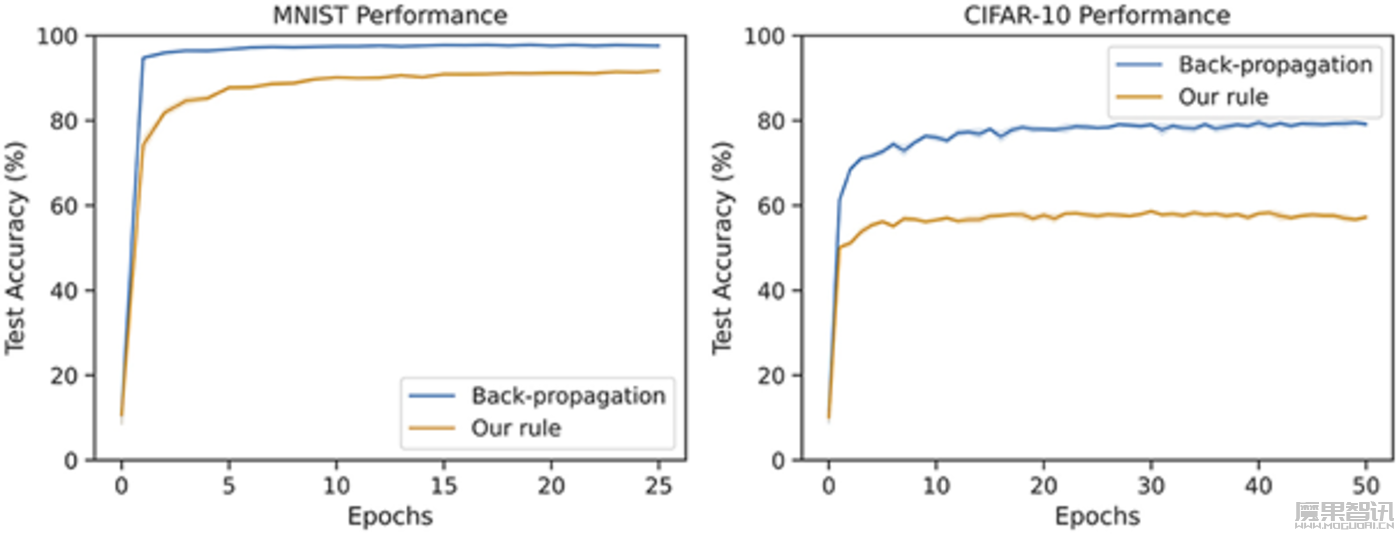
▷图3:在MNIST和CIFAR-10数据集上,研究者对反向传播和信息瓶颈方法进行了多次测试,并计算了平均测试准确度。MNIST网络是一个具有128和64隐藏神经元的全连接感知机。CIFAR-10网络是一个具有128和256特征的卷积,之后是一个单一的完全连接的输出层。
工作记忆是我们认知系统中至关重要的一部分,它使我们能在回忆存储的知识和经验的同时,继续进行其他任务。在实验中,当模型的工作记忆容量从最初的仅能处理2幅图片信息增加到能处理32幅图片时,模型的预测准确度有所提升,且学习率也有提升——即所需的训练轮次减少。然而,记忆容量的增长和性能提升之间存在对数关系,暗示着收益递减的效应。这一现象为工作记忆的容量与学习效率之间的关系提供了实证支持。
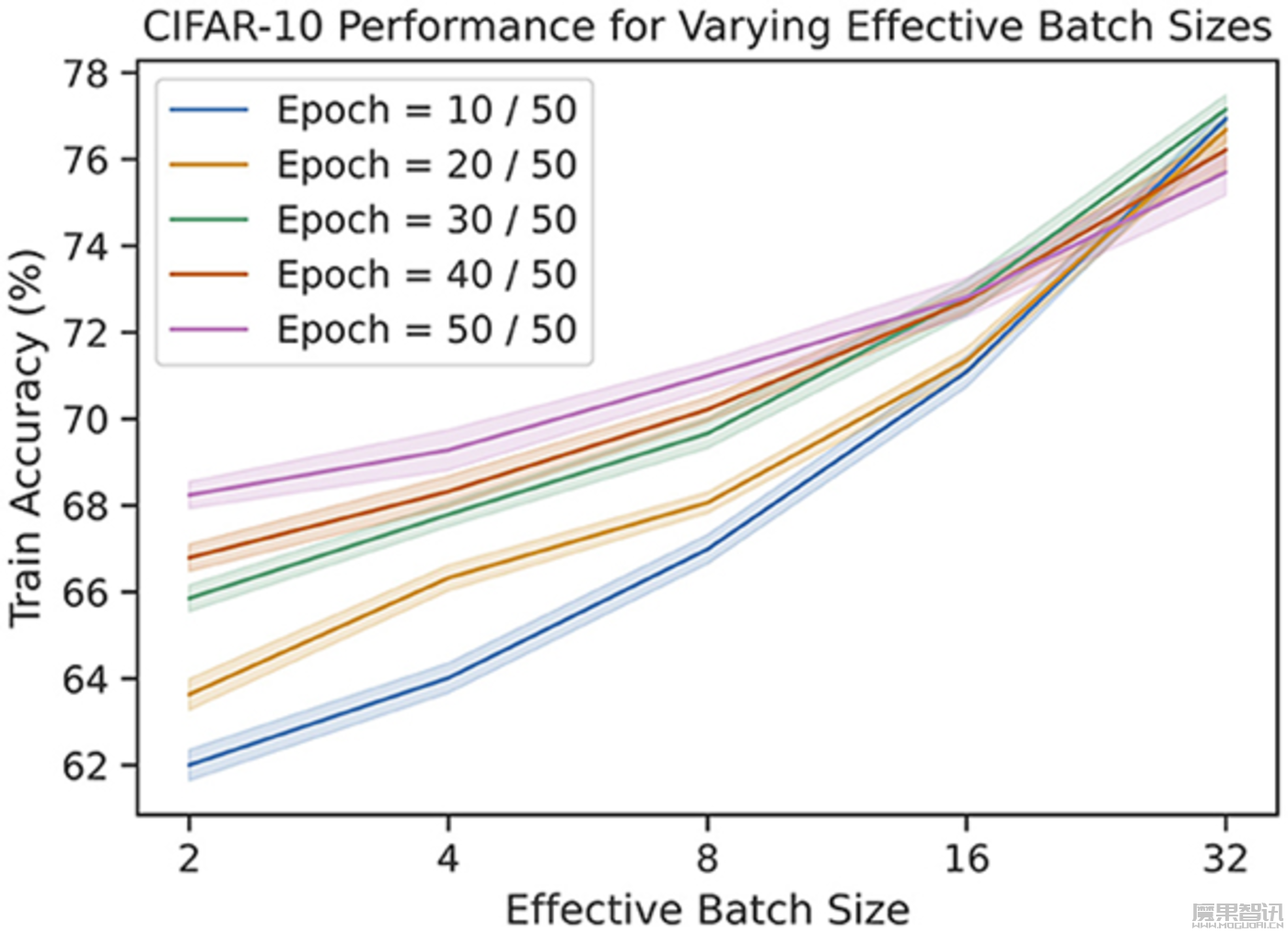
虽然相比传统的反向传播,基于信息瓶颈的模型在准确度上仍有差距,但这种模型能够让学习系统实时接收反馈,更贴近生物学上的学习机制。在我们的大脑中,神经元间的连接一直在变化和调整,这并不是说你可以暂停一切,调整,然后继续做你自己。
反向传播的训练和实际应用是分开的,仿佛是学生在一个学期内集中学习,然后在考试中检验所学,而在学习阶段,我们无法对它的水平进行实时判断。而基于信息瓶颈的新模型则类似于人类的学习方式,就像小孩在看到一个新图像时询问父母这是什么,即使父母未能回答,孩子也能依据以往的经验和反馈进行推断。这种‘即插即用’的过程,更适应生物通过自然选择的方式,对于需要快速反应的任务尤其有效。
尽管还没有证据说明类似图2的网络结构在脑中真实存在,但该研究提出的基于信息瓶颈和局部可塑性(赫布法则)的模型,已被证明可以在复杂的大数据上进行学习,以及在执行简单非线性函数的分类任务上达到近乎完美的准确性。由此,可说明该模型提供了一种新的,不依赖反向传播的学习方法,并首次将工作记忆和突触权重联系起来,这可能为下一代人工智能的发展提供启发。









